Page 50 - ITU Journal Future and evolving technologies Volume 2 (2021), Issue 4 – AI and machine learning solutions in 5G and future networks

ITU Journal on Future and Evolving Technologies, Volume 2 (2021), Issue 4

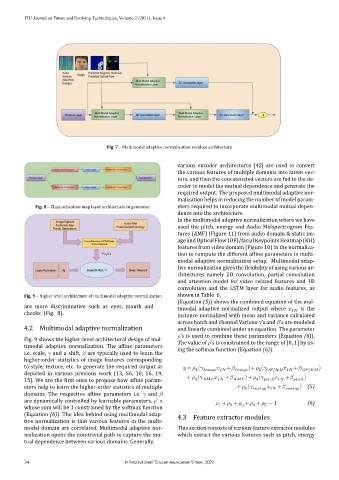
Fig. 7 – Multimodal adaptive normalization residual architecture

various encoder architectures [42] are used to convert
the various features of multiple domains into latent vec‑
tors, and then the concatenated vectors are fed to the de‑
coder to model the mutual dependence and generate the
required output. The proposed multimodal adaptive nor‑
malization helps in reducing the number of model param‑
Fig. 8 – Class activation map layer architecture in generator eters required to incorporate multimodal mutual depen‑
dence into the architecture.
In the multimodal adaptive normalization where we have
used the pitch, energy and Audio Melspectrogram Fea‑
tures (AMF) (Figure 11) from audio domain & static im‑
ageandOpticalFlow(OF)/facialKeypointsHeatmap(KH)
features from video domain (Figure 10) in the normaliza‑
tion to compute the different af ine parameters in multi‑
modal adaptive normalization setup. Multimodal adap‑
tive normalization gives the lexibility of using various ar‑
chitectures namely 2D convolution, partial convolution
and attention model for video related features and 1D
convolution and the LSTM layer for audio features, as
Fig. 9 – Higher level architecture of multimodal adaptive normalization shown in Table 6.
(Equation (5)) shows the combined equation of the mul‑
timodal adaptive normalized output where is the

(Fig. 8). instance normalized with mean and variance calculated
across batch and channel.Various ’s and ’s are modeled
4.2 Multimodal adaptive normalization and linearly combined under an equation. The parameter
’s is used to combine these parameters (Equation (6)).
Fig. 9 shows the higher‑level architectural design of mul‑
The value of ’s is constrained to the range of [0, 1] by us‑
timodal adaptive normalization. The ine parameters
ing the softmax function (Equation (6)).
i.e, scale, and a shift, are typically used to learn the
higher‑order statistics of image features corresponding

to style, texture, etc. to generate the required output as = ( + )+ ( / + / )

2
1
depicted in various previous work [13, 56, 18, 16, 19,
+ ( + )+ ( + )
15]. We are the irst ones to propose how af ine param‑ 3 4 ℎ ℎ

eters help to learn the higher‑order statistics of multiple + ( + ) (5)
5
domains. The respective af ine parameters i.e. and
are dynamically controlled by learnable parameters, ’ s + + + + = 1 (6)
3
5
4
2
1
whose sum will be 1 constrained by the softmax function
(Equation (6)). The idea behind using multimodal adap‑ 4.3 Feature extractor modules
tive normalization is that various features in the multi‑
modal domain are correlated. Multimodal adaptive nor‑ This section consists of various feature extractor modules
malization opens the non‑trivial path to capture the mu‑ which extract the various features such as pitch, energy
tual dependence between various domains. Generally,
34 © International Telecommunication Union, 2021