Page 53 - ITU Journal, Future and evolving technologies - Volume 1 (2020), Issue 1, Inaugural issue

ITU Journal on Future and Evolving Technologies, Volume 1 (2020), Issue 1

0.8 1 1 1
0.5 0.5 0.5
0.6
0 0 0
0.4
-0.5 -0.5 -0.5
0.2 -1 -1 -1
Amplitude 0 0 50 100 Approximation 200 250 300 0 50 100 Approximation 200 250 300 0 50 100 Approximation 200 250 300
150
150
150
-0.2 0.2 0.2 0.1
0.1 0.05
-0.4 0.1
0 0
-0.6 0
-0.1 -0.05
-0.8 -0.1 -0.2 -0.1
0 100 200 300 400 500 600 0 50 100 150 200 250 300 0 50 100 150 200 250 300 0 50 100 150 200 250 300
Audio Signal Detail Detail Detail
(a) (b) (c) (d)
1 1 1 1
0.5 0.5 0.5 0.5
0 0 0 0
-0.5 -0.5 -0.5 -0.5
-1 -1 -1 -1
0 50 100 150 200 250 300 0 50 100 150 200 250 300 0 50 100 150 200 250 300 0 20 40 60 80 100 120 140 160 180 200
Approximation Approximation Approximation Approximation
0.1 0.2 0.1 0.2
0.05 0.1 0.05 0.1
0 0 0 0
-0.05 -0.1 -0.05 -0.1
-0.1 -0.2 -0.1 -0.2
0 50 100 150 200 250 300 0 50 100 150 200 250 300 0 50 100 150 200 250 300 0 20 40 60 80 100 120 140 160 180 200
Detail Detail Detail Detail
(e) (f) (g) (h)
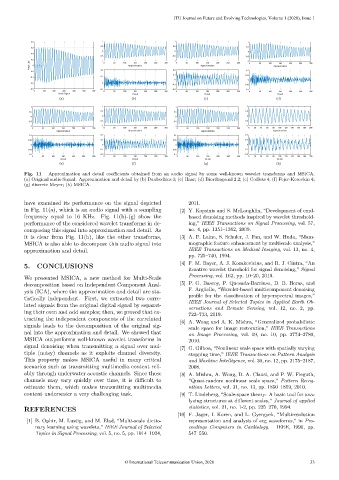
Fig. 11 – Approximation and detail coefficients obtained from an audio signal by some well-known wavelet transforms and MSICA.
(a) Original audio Signal. Approximation and detail by (b) Daubechies 3; (c) Haar; (d) Biorthogonal 2.2; (e) Coiflets 4; (f) Fejer-Korovkin 4;
(g) discrete Meyer; (h) MSICA.
have examined its performance on the signal depicted 2011.
in Fig. 11(a), which is an audio signal with a sampling [2] Y. Kopsinis and S. McLaughlin, “Development of emd-
frequency equal to 16 KHz. Fig. 11(b)-(g) show the based denoising methods inspired by wavelet threshold-
performance of the considered wavelet transforms in de- ing,” IEEE Transactions on Signal Processing, vol. 57,
composing this signal into approximation and detail. As no. 4, pp. 1351–1362, 2009.
it is clear from Fig. 11(h), like the other transforms, [3] A. F. Laine, S. Schuler, J. Fan, and W. Huda, “Mam-
MSICA is also able to decompose this audio signal into mographic feature enhancement by multiscale analysis,”
approximation and detail. IEEE Transactions on Medical Imaging, vol. 13, no. 4,
pp. 725–740, 1994.
5. CONCLUSIONS [4] F. M. Bayer, A. J. Kozakevicius, and R. J. Cintra, “An
iterative wavelet threshold for signal denoising,” Signal
We presented MSICA, a new method for Multi-Scale Processing, vol. 162, pp. 10–20, 2019.
decomposition based on Independent Component Anal- [5] P. G. Bascoy, P. Quesada-Barriuso, D. B. Heras, and
ysis (ICA), where the approximation and detail are sta- F. Argüello, “Wavelet-based multicomponent denoising
tistically independent. First, we extracted two corre- profile for the classification of hyperspectral images,”
IEEE Journal of Selected Topics in Applied Earth Ob-
lated signals from the original digital signal by separat- servations and Remote Sensing, vol. 12, no. 2, pp.
ing their even and odd samples; then, we proved that ex- 722–733, 2019.
tracting the independent components of the correlated [6] A. Wong and A. K. Mishra, “Generalized probabilistic
signals leads to the decomposition of the original sig- scale space for image restoration,” IEEE Transactions
nal into the approximation and detail. We showed that on Image Processing, vol. 19, no. 10, pp. 2774–2780,
MSICA outperforms well-known wavelet transforms in 2010.
signal denoising when transmitting a signal over mul- [7] G. Gilboa, “Nonlinear scale space with spatially varying
tiple (noisy) channels as it exploits channel diversity. stopping time,” IEEE Transactions on Pattern Analysis
This property makes MSICA useful in many critical and Machine Intelligence, vol. 30, no. 12, pp. 2175–2187,
scenarios such as transmitting multimedia content reli- 2008.
ably through underwater acoustic channels. Since these [8] A. Mishra, A. Wong, D. A. Clausi, and P. W. Fieguth,
channels may vary quickly over time, it is difficult to “Quasi-random nonlinear scale space,” Pattern Recog-
estimate them, which makes transmitting multimedia nition Letters, vol. 31, no. 13, pp. 1850–1859, 2010.
content underwater a very challenging task. [9] T. Lindeberg, “Scale-space theory: A basic tool for ana-
lyzing structures at different scales,” Journal of applied
REFERENCES statistics, vol. 21, no. 1-2, pp. 225–270, 1994.
[10] F. Jager, I. Koren, and L. Gyergyek, “Multiresolution
[1] B. Ophir, M. Lustig, and M. Elad, “Multi-scale dictio- representation and analysis of ecg waveforms,” in Pro-
nary learning using wavelets,” IEEE Journal of Selected ceedings Computers in Cardiology. IEEE, 1990, pp.
Topics in Signal Processing, vol. 5, no. 5, pp. 1014–1024, 547–550.

© International Telecommunication Union, 2020 33