Page 126 - ITU Journal, ICT Discoveries, Volume 3, No. 1, June 2020 Special issue: The future of video and immersive media

ITU Journal: ICT Discoveries, Vol. 3(1), June 2020

large for 27 comparisons (r > 0.5), medium to large in
2.5
58 comparisons (0.3 < r ≤ 0.5), and small to medium in
2 94 comparisons (0.1 < r ≤ 0.3). The largest effect size
observed (r = 0.63) corresponds to the difference between
1.5
the U−090 / M+180 direction pair.
1
Table 4 – Summary of significant differences spotted on pairwise
0.5
comparisons of directional loudness sensitivities among source
directions.
0
-0.5 Directions Very significant Significant Total
(θ,φ) (p < 0.01) (p < 0.05) differences
-1 ◦ ◦
(−45 ,−30 ) 2 1 3
◦
◦
-1.5 (0 ,−30 ) 3 8 11
1 2 3 4 5 6 7 8 9 10 11 12 ◦ ◦
(45 ,−30 ) 2 2 4
◦
◦
(−135 ,0 ) 0 3 3
◦
◦
Fig. 2 – Means and 95% confidence intervals of subject scores (−90 ,0 ) 3 3 6
◦
◦
(DLS). (−60 ,0 ) 2 2 4
◦
◦
(−30 ,0 ) 0 2 2
◦
◦
(0 ,0 ) 0 2 2
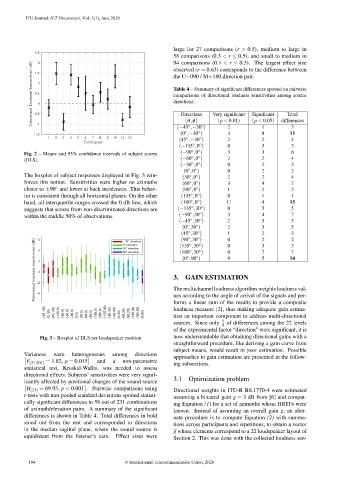
The boxplot of subject responses displayed in Fig. 3 rein- (30 ,0 ) 2 2 4
◦
◦
forces this notion. Sensitivities were higher on azimuths (60 ,0 ) 3 4 7
◦
◦
◦
◦
◦
closer to ±90 and lower at back incidences. This behav- (90 ,0 ) 1 2 3
◦
◦
ior is consistent through all horizontal planes. On the other (135 ,0 ) 0 1 1
◦
◦
hand, all interquartile ranges crossed the 0 dB line, which (180 ,0 ) 11 4 15
◦
◦
suggests that scores from non-discriminated directions are (−135 ,30 ) 0 5 5
◦
◦
within the middle 50% of observations. (−90 ,30 ) 3 4 7
◦
◦
(−45 ,30 ) 2 3 5
◦
◦
(0 ,30 ) 2 3 5
◦
◦
(45 ,30 ) 1 2 3
◦ ◦
6 (90 ,30 ) 0 2 2
◦
◦
(135 ,30 ) 0 3 3
4 ◦ ◦
(180 ,30 ) 0 7 7
◦
◦
(0 ,90 ) 9 5 14
2
0
3. GAIN ESTIMATION
-2
The multichannel loudness algorithm weights loudness val-
-4
ues according to the angle of arrival of the signals and per-
forms a linear sum of the results to provide a composite
(-45,-30) (0,-30) (45,-30) (-135,0) (-90,0) (-60,0) (-30,0) (0,0) (30,0) (60,0) (90,0) (135,0) (180,0) (-135,30) (-90,30) (-45,30) (0,30) (45,30) (90,30) (135,30) (180,30) (0,90) loudness measure [2], thus making adequate gain estima-
tion an important component to address multi-directional
sources. Since only 1 of differences among the 22 levels
4
of the experimental factor “direction” were significant, it is
Fig. 3 – Boxplot of DLS per loudspeaker position now understandable that obtaining directional gains with a
straightforward procedure, like deriving a gain curve from
subject means, would result in poor estimation. Possible
Variances were heterogeneous among directions
approaches to gain estimation are presented in the follow-
F (21,501) = 1.82, p = 0.015 and a non-parametric ing subsections.
statistical test, Kruskal-Wallis, was needed to assess
directional effects. Subjects’ sensitivities were very signif-
icantly affected by positional changes of the sound source 3.1 Optimization problem

H (21) = 69.93, p < 0.001 . Pairwise comparisons using Directional weights in ITU-R BS.1770-4 were estimated
t-tests with non-pooled standard deviations spotted statisti- assuming a binaural gain g = 3 dB from [6] and comput-
cally significant differences in 58 out of 231 combinations ing Equation (1) for a set of azimuths whose HRTFs were
of azimuth/elevation pairs. A summary of the significant known. Instead of assuming an overall gain g, an alter-
differences is shown in Table 4. Total differences in bold nate procedure is to compute Equation (2) with summa-
stood out from the rest and corresponded to directions tions across participants and repetitions, to obtain a vector
in the median sagittal plane, where the sound source is ~g whose elements correspond to a 22 loudspeaker layout of
equidistant from the listener’s ears. Effect sizes were Section 2. This was done with the collected loudness sen-
104 © International Telecommunication Union, 2020