Page 103 - Kaleidoscope Academic Conference Proceedings 2024

BENCHMARKING MATRIX MULTIPLICATIONS FOR VARIABLE QUBIT SIZE AND
DEPTH

1
1
1
1
1
Md Imam Mazhar ; Abhishek Tiwari ; Nasir Ali ; Britant ; Akshay Patil ; Rahul Kumar Neiwal 2
1
Embedded Systems Division, Centre for Development of Advanced Computing (C-DAC), Noida
2
Ministry of Electronics and Information Technology (MeitY), New Delhi
ABSTRACT
To emulate a quantum computation on a classical computer
i.e. the evolution of the unitary operations on the wave
function of the particle in quantum mechanics, we have to
perform unitary matrix and normalized vector multiplications
in the high-level programming languages of Python, C++,
Java, etc. Quantum Libraries already available perform the
matrix-vector multiplication in the backend using the numpy
libraries of Python like Qiskit or use a C++ wrapper to
further optimize the runtime it as in Qiskit-Aer Simulators.
Since a fully functioning fault-tolerant computer is decades
away, it is in our best interest to design new quantum
algorithms and develop accelerator test beds for Quantum
Emulations. All the quantum computer operations can be
emulated on a classical computer, with the only downside
3
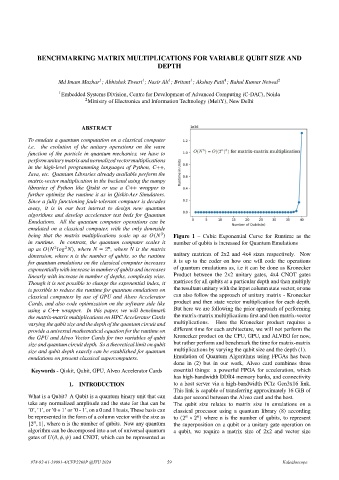
being that the matrix multiplications scale up as ( ) Figure 1 – Cubic Exponential Curve for Runtime as the
in runtime. In contrast, the quantum computer scales it number of qubits is increased for Quantum Emulations
2
2
up as ( ), where N = 2 , where N is the matrix

dimension, where n is the number of qubits, so the runtime unitary matrices of 2x2 and 4x4 sizes respectively. Now
for quantum emulations on the classical computer increases it is up to the coder on how one will code the operations
exponentially with increase in number of qubits and increases of quantum emulations as, i.e it can be done as Kronecker
linearly with increase in number of depths, complexity wise. Product between the 2x2 unitary gates, 4x4 CNOT gates
Though it is not possible to change the exponential index, it matrices for all qubits at a particular depth and then multiply
is possible to reduce the runtime for quantum emulations on the resultant unitary with the input column state vector, or one
classical computers by use of GPU and Alveo Accelerator can also follow the approach of unitary matrix - Kronecker
Cards, and also code optimization on the software side like product and then state vector multiplication for each depth.
using a C++ wrapper. In this paper, we will benchmark But here we are following the prior approach of performing
the matrix-matrix multiplications on HPC Accelerator Cards the matrix-matrix multiplications first and then matrix-vector
varying the qubit size and the depth of the quantum circuit and multiplications. Here the Kronecker product requires a
different time for each architecture, we will not perform the
provide a universal mathematical equation for the runtime on
the GPU and Alveo Vector Cards for two variables of qubit Kronecker product on the CPU, GPU, and ALVEO for now,
size and quantum circuit depth. So a theoretical limit on qubit but rather perform and benchmark the time for matrix-matrix
size and qubit depth exactly can be established for quantum multiplications by varying the qubit size and the depth (1).
emulations on present classical supercomputers. Emulation of Quantum Algorithms using FPGAs has been
done in (2) but in our work, Alveo card combines three
Keywords - Qiskit, Qubit, GPU, Alveo Accelerator Cards essential things: a powerful FPGA for acceleration, which
has high-bandwidth DDR4 memory banks, and connectivity
1. INTRODUCTION to a host server via a high-bandwidth PCIe Gen3x16 link.
This link is capable of transferring approximately 16 GiB of
What is a Qubit? A Qubit is a quantum binary unit that can data per second between the Alveo card and the host.
take any normalized amplitude and the state for that can be The qubit size relates to matrix size in emulations on a
’0’, ’1’, or ’0 + 1’ or ’0 - 1’, on a 0 and 1 basis, These basis can classical processor using a quantum library (8) according
be represented in the form of a column vector with the size as to (2 ∗ 2 ) where n is the number of qubits, to represent

[2 , 1], where n is the number of qubits. Now any quantum the superposition on a qubit or a unitary gate operation on
algorithm can be decomposed into a set of universal quantum a qubit, we require a matrix size of 2x2 and vector size
gates of ( , , ) and CNOT, which can be represented as

978-92-61-39091-4/CFP2268P @ITU 2024 – 59 – Kaleidoscope