Page 82 - ITU Journal Future and evolving technologies Volume 2 (2021), Issue 7 – Terahertz communications

ITU Journal on Future and Evolving Technologies, Volume 2 (2021), Issue 7

0 5 5
0 5 0
0
0.5 0
0
0.5 0.5
-5
-5 1 -5
1 -10 1 -10
Width (m) 1.5 -10 -15 Width (m) 1.5 -15 Width (m) 1.5 -15
2 2 2
-20
-20 -20
2.5 2.5 -25 2.5
-25 -25
3 -30 3 -30 3 -30
0 0.5 1 1.5 2 2.5 3 3.5 4 4.5 5 0 0.5 1 1.5 2 2.5 3 3.5 4 4.5 5 0 0.5 1 1.5 2 2.5 3 3.5 4 4.5 5
Length (m) Length (m) Length (m)
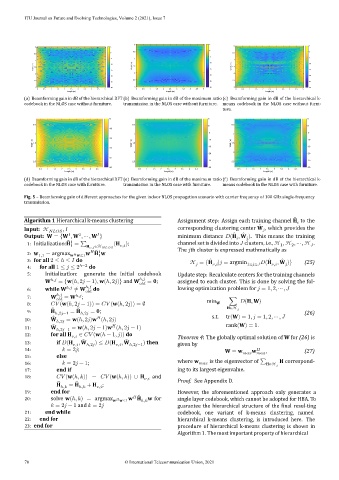
(a) Beamforming gain in dB of the hierarchical DFT (b) Beamforming gain in dB of the maximum ratio (c) Beamforming gain in dB of the hierarchical k‑
codebook in the NLOS case without furniture. transmission in the NLOS case without furniture. means codebook in the NLOS case without furni‑
ture.
-5 5 5
0.5 0.5 0.5
0 0
-10
-5 -5
1 1 1
-15 -10 -10
Width (m) 1.5 Width (m) 1.5 Width (m) 1.5
-20 -15 -15
2 2 2
-20 -20
-25
-25 -25
2.5 2.5 2.5
-30 -30 -30
0.5 1 1.5 2 2.5 3 3.5 4 4.5 0.5 1 1.5 2 2.5 3 3.5 4 4.5 0.5 1 1.5 2 2.5 3 3.5 4 4.5
Length (m) Length (m) Length (m)
(d) Beamforming gain in dB of the hierarchical DFT (e) Beamforming gain in dB of the maximum ratio (f) Beamforming gain in dB of the hierarchical k‑
codebook in the NLOS case with furniture. transmission in the NLOS case with furniture. means codebook in the NLOS case with furniture.
Fig. 5 – Beamforming gain of different approaches for the given indoor NLOS propagation scenario with carrier frequency of 100 GHz single‑frequency
transmission.
̂
Algorithm 1 Hierarchical k‑means clustering Assignment step: Assign each training channel H to the

̂
Input: ℋ , corresponding clustering center W , which provides the

̂
̂

1
2
Output: W = {W , W , ⋯ , W } minimum distance (H , W ). This means the training

̃ 1
1: Initialization:H = ∑ H , ∈ℋ (H , ); channel set is divided into clusters, i.e., ℋ , ℋ , ⋯ , ℋ .
1
2

1
̃ 1
2: w 1,1 = argmax w w≤1 w H w The th cluster is expressed mathmatically as

1
3: for all 2 ≤ ℎ ≤ do ℋ = {H ̂ , | = argmin 1≤ ≤ (H ̂ , , W )} (25)
̂

4: for all 1 ≤ ≤ 2 ℎ−2 do
5: Initialization: generate the initial codebook Update step: Recalculate centers for the training channels
W ℎ, = {w(ℎ, 2 − 1), w(ℎ, 2 )} and W ℎ, = 0; assigned to each cluster. This is done by solving the fol‑

6: while W ℎ, ≠ W ℎ, do lowing optimization problem for = 1, 2, ⋯ ,

7: W ℎ, = W ℎ, ; min ∑ (H, W)

8: (w(ℎ, 2 − 1)) = (w(ℎ, 2 )) = ∅ W
9: H ̃ ℎ,2 −1 = H ̃ ℎ,2 = 0; H∈ℋ (26)

10: W ̂ ℎ,2 = w(ℎ, 2 )w (ℎ, 2 ) s.t. tr(W) = 1, = 1, 2, ⋯ ,

11: W ̂ ℎ,2 −1 = w(ℎ, 2 − 1)w (ℎ, 2 − 1) rank(W) = 1.
12: for all H , ∈ (w(ℎ − 1, )) do Theorem 4: The globally optimal solution of W for (26) is
13: if (H , , W ̂ ℎ,2 ) ≤ (H , , W ̂ ℎ,2 −1 ) then given by
14: = 2 ; W = w w , (27)

15: else
16: = 2 − 1; where w is the eigenvector of ∑ H∈ℋ H correspond‑
17: end if ing to its largest eigenvalue.
18: (w(ℎ, )) = (w(ℎ, )) ∪ H , and Proof. See Appendix D.
H ̃ ℎ, = H ̃ ℎ, + H , ;
19: end for However, the aforementioned approach only generates a
̃
20: solve w(ℎ, ) = argmax w w≤1 w H ℎ, w for single layer codebook, which cannot be adopted for HBA. To

= 2 − 1 and = 2 guarantee the hierarchical structure of the inal resul-ting
21: end while codebook, one variant of k‑means clustering, named
22: end for hierarchical k‑means clustering, is introduced here. The
23: end for procedure of hierarchical k‑means clustering is shown in
Algorithm 1. The most important property of hierarchical
70 © International Telecommunication Union, 2021