Page 72 - ITU Journal: Volume 2, No. 1 - Special issue - Propagation modelling for advanced future radio systems - Challenges for a congested radio spectrum

ITU Journal: ICT Discoveries, Vol. 2(1), December 2019

When increases, the validity conditions of SPM
given in Equation (11) are not satisfied, and
Equation (12) cannot be used. The next bi-static
scattering coefficients to be used are those based on
a physical optics model.

4. DIFFUSE BI-STATIC SCATTERING
COEFFICIENT BASED ON THE
PHYSICAL OPTICS (PO) MODEL
The validity conditions of PO are given by Equation
(17) of [4].
ℓ > 6, and ℓ > 5.893 (17)

̂ ̂
The diffuse bi-static scattering coefficient ( , )

from randomly rough surface based on physical
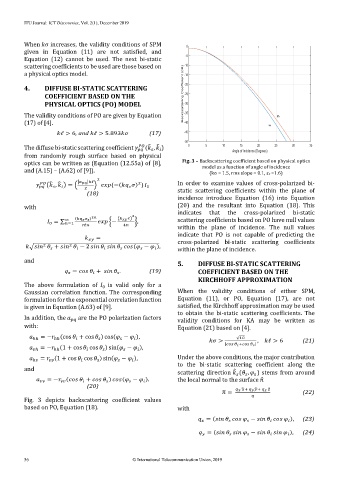
optics can be written as (Equation (12.55a) of [8], Fig. 3 – Backscattering coefficient based on physical optics
model as a function of angle of incidence
and (A.15) – (A.62) of [9]). (kσ = 1.5, rms slope = 0.1, εr =1.6)
2
2
̂ ̂ | | ℓ ) {−( ) } In order to examine values of cross-polarized bi-
( , ) = (

2 0
(18) static scattering coefficients within the plane of
incidence introduce Equation (16) into Equation
with (20) and the resultant into Equation (18). This
indicates that the cross-polarized bi-static
2
= ∑ ∞ ( ) 2 {− ( ℓ) }, scattering coefficients based on PO have null values
0
=1
!
4
within the plane of incidence. The null values
indicate that PO is not capable of predicting the
=
√ + − 2 ( − ), cross-polarized bi-static scattering coefficients
2
2
within the plane of incidence.

and 5. DIFFUSE BI-STATIC SCATTERING
= + . (19) COEFFICIENT BASED ON THE

KIRCHHOFF APPROXIMATION
The above formulation of is valid only for a
0
Gaussian correlation function. The corresponding When the validity conditions of either SPM,
formulation for the exponential correlation function Equation (11), or PO, Equation (17), are not
is given in Equation (A.63) of [9]. satisfied, the Kirchhoff approximation may be used
to obtain the bi-static scattering coefficients. The
In addition, the are the PO polarization factors validity conditions for KA may be written as

with: Equation (21) based on [4].
ℎℎ = − (cos + cos ) cos( − ), > √10 , ℓ > 6 (21)

ℎℎ

ℎ = − (1 + cos cos ) sin( − ), | + |
ℎℎ

ℎ = (1 + cos cos ) sin( − ), Under the above conditions, the major contribution

and to the bi-static scattering coefficient along the
̂
scattering direction ( , ) stems from around

= − ( + ) ( − ). the local normal to the surface ̂

(20)
̂ = ̂ + ̂+ ̂ (22)

Fig. 3 depicts backscattering coefficient values
based on PO, Equation (18). with
= ( − ), (23)

= ( − ), (24)

56 © International Telecommunication Union, 2019