Page 127 - Proceedings of the 2018 ITU Kaleidoscope

Machine learning for a 5G future

(a) Linearly separable classes. (b) Maximum margin.
Figure 5 – Overfitted samples
where ρ is the margin width, ξ i is the cost paid of the ith
violating sample and C is a parameter that enables to tune the
tradeoff between the width of the margin and the amount of
violating samples.
If C is large, there will be fewer training errors, meaning
that fewer samples from the training set will be misclassified,
also known as overfitting. When overfitting occurs, as shown
by the dashed line in Fig. 5, classes are perfectly separated,
but the separation is greatly influenced by noise, potentially
leading to greater classification errors.
(c) Margin violation and
On the contrary, when C is small, there will be more
misclassification.
misclassified samples, but the margin will be greater, as
Figure 4 – SVM using a linear classifier showed by the grey continuous line in Fig. 5. To improve the
final result of the algorithm this parameter has to be chosen
and M is the number of classes in the problem. using cross-validation[8].

1.6 Support Vector Machine 1.7 Comparison

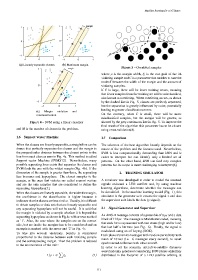
When the classes are linearly separable, a straight line can be The selection of the best algorithm heavily depends on the
drawn that perfectly separates the classes and the margin is nature of the problem and the features used. Nevertheless,
the perpendicular distance between the closest points to the SVM is less computationally demanding than kNN and is
line from each class as seen in Fig. 4a. This method is called easier to interpret but can identify only a limited set of
Support vector Machine (SVM)[12]. Nevertheless, many patterns. On the other hand, kNN can find very complex
possible separating lines exists that separates the classes and patterns but its output is more challenging to interpret[6].
SVM finds the one with the widest margin (Fig. 4b). If the
dimension of the sample is greater than three, the separating 2. TRAINING SIMULATOR
line becomes and hyperplane. The closest samples to the
margin, or the ones that violates are called support vectors A simulator was developed in order to model the received
and are the only samples that are considered to define the signals on-board a LEO satellite and, by using machine
separating hyperplane[7]. learning algorithms, determine whether the messages can
When the classes are linearly separable, the wider the margin, be decodified. In the machine learning model (Fig. 1), this
the confidence in the classification is higher because it simulator is the generator as it creates the signal x and also
indicates that the classes are less similar. Usually, it is difficult the supervisor as it labels the data (y signal).
to obtain samples or data sets that are linearly separable and
any separating hyperplane will not be useful. It is said that 2.1 Signal Generator and Supervisor
the margin is violated by a sample whether it is beyond the
An ADS-B message consists of a preamble of 8µs and a data
separating hyperplane as shown in Fig 4c with arrows marked
block of 112µs. The message is Manchester-coded, meaning
as ‘1’. Also, the case where the samples are on the correct
that each bit is represented with two states (high and/or low)
side, but are inside the margins has to be considered and an
that last half a bit time (see Fig. 6). Finally, the signal is
example is marked with the arrow and ‘2’ in Fig. 4c.
modulated using on-off keying (OOK).
To take into account violations, penalty is considered
Each plane transmits messages with random periodicity with
proportional to the distance between each violating sample
mean of 161ms (i.e. 6 messages every second), to avoid
and the corresponding margin. Then the problem is reduced
synchronized collisions with other aircraft.
to the minimization of the risk::
In order to set the scenario, aircraft-to-satellite distances
were randomly generated considering 1000 planes uniformly
Õ
1/ρ + C ξ i (5) distributed in the footprint of a LEO satellite orbiting at
– 111 –