Page 88 - ITU Journal Future and evolving technologies Volume 2 (2021), Issue 7 – Terahertz communications

ITU Journal on Future and Evolving Technologies, Volume 2 (2021), Issue 7

The reason is that the NLOS channel suffers from strong
10 0
frequency‑selectivity. Thus, the training channels within
the same beam coverage may have a large distance, which
10 -1
might direct the HBA to a non‑optimal code. Besides,
the reduced channel quality in the NLOS case increases
10 -2
the misalignment rate signi icantly. However, this perfor‑
BER 10 -3 mance degradation is less than 1 dB, which is acceptable
compared to the high exploration cost for the exhaustive
search.
Exhaustive search
10 -4
HBA
Optimal beamforming
10 -5 Random beamforming 6. CONCLUSION
Exp3
-10 -5 0 5 10 15 20 25 In this paper, hierarchical beam alignment with hierar‑
SNR (dB)
chical codebook design for SU‑MIMO THz communica‑
Fig. 10 – Average BER vs. SNR for different beamforming schemes in tions has been studied. First, the hierarchical codebook
LOS scenario. design problem in MIMO THz communications has been
achieves a performance close to that of the optimal beam‑ established. Next, the hierarchical codebooks for LOS
forming and exhaustive search, respectively, which com‑ and NLOS propagation have been designed based on DFT
codebook and data‑driven hierarchical k‑means cluste-
plies with Theorem 2 and demonstrates the bene its of
ring, respectively. Then, the beam alignment problem
the HBA. In addition, although the Exp3 algorithm can
in THz communications has been formulated and the
achieve a similar BER performance as the HBA, Exp3 re‑
HBA from mmWave communications is adjusted to
quires double the number of the time slots than HBA.
the SC‑FDMA SU‑MIMO THz communication system.
Hence, HBA is able to provide a close‑to‑optimal beam se‑
Numerical results show that HBA combined with
lection with signi icantly shorter latency in the LOS sce‑
hierarchical DFT codebook can achieve a performance
nario compared to the benchmark schemes.
close to the optimal beamforming from [10] in a LOS
0 scenario, while in an NLOS scenario HBA combined with
10
hierarchical k‑means codebook outperforms the DFT
codebook. In our future work, the HBA will be extended
-2
10 to a multi‑user transmis‑ sion.
BER 10 -4 APPENDIX A
H-kmeans full searching
Random beamforming Proof of Theorem 1
10 -6 DFT HBA
H.kmeans HBA
Opt beamforming Here, the maximum over the codebook can be replaced by
H-kmeans Exp3 the ‑norm as
10 -8 ∞
-5 0 5 10 15 20 25
SNR (dB)

2

2
∫max w∈W ‖a ( , )w‖ = ∫‖a ( , )W ‖

∞

2
Fig. 11 – Average BER vs. SNR for different beamforming schemes in
NLOS scenario. (42)
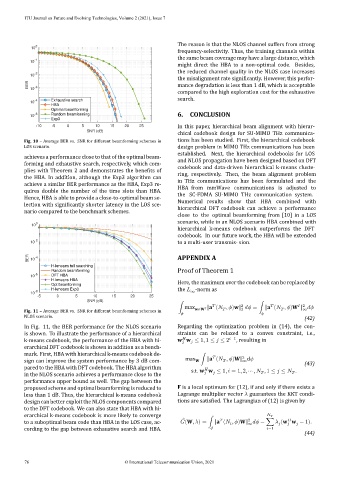
In Fig. 11, the BER performance for the NLOS scenario Regarding the optimization problem in (14), the con‑
is shown. To illustrate the performance of a hierarchical straints can be relaxed to a convex constraint, i.e.,

k‑means codebook, the performance of the HBA with hi‑ w w ≤ 1, 1 ≤ ≤ 2 −1 , resulting in

erarchical DFT codebook is shown in addition as a bench‑
mark. First, HBA with hierarchical k‑means codebook de‑ 2
sign can improve the system performance by 3 dB com‑ max ∫ ‖a ( , )W‖ d (43)
W

∞
pared to the HBA with DFT codebook. The HBA algorithm s.t. w w ≤ 1, = 1, 2, ⋯ , , 1 ≤ ≤ .

in the NLOS scenario achieves a performance close to the
performance upper bound as well. The gap between the
proposed scheme and optimal beamforming is reduced to F is a local optimum for (12), if and only if there exists a
less than 1 dB. Thus, the hierarchical k‑means codebook Lagrange multiplier vector guarantees the KKT condi‑
design can better exploit the NLOS components compared tions are satis ied. The Lagrangian of (12) is given by
to the DFT codebook. We can also state that HBA with hi‑
erarchical k‑means codebook is more likely to converge
̂

2

to a suboptimal beam code than HBA in the LOS case, ac‑ (W, ) = ∫‖a ( , )W‖ − ∑ (w w − 1).

∞

cording to the gap between exhaustive search and HBA. =1
(44)
76 © International Telecommunication Union, 2021