Page 136 - ITU Journal Future and evolving technologies Volume 2 (2021), Issue 3 – Internet of Bio-Nano Things for health applications

ITU Journal on Future and Evolving Technologies, Volume 2 (2021), Issue 3

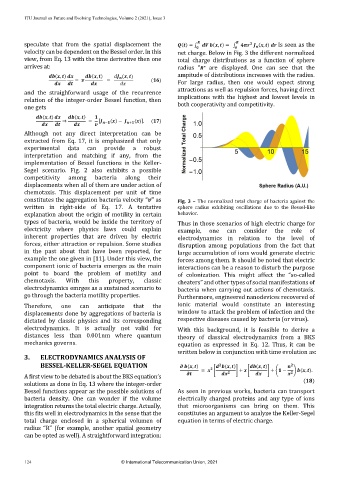
speculate that from the spatial displacement the ( ) = ∫ ( , ) = ∫ ( , ) Is seen as the

velocity can be dependent on the Bessel order. In this net charge. Below in Fig. 3 the different normalized
view, from Eq. 13 with the time derivative then one total charge distributions as a function of sphere
arrives at: radius " " are displayed. One can see that the
( , ) ( , ) ( , ) ampitude of distributions increases with the radius.
= = ( )
For large radius, then one would expect strong
and the straighforward usage of the recurrence attractions as well as repulsion forces, having direct
relation of the integer-order Bessel function, then implications with the highest and lowest levels in
one gets both cooperativity and competitivity.
( , ) ( , )
⇒ = [ − ( ) − + ( )]. ( )

Although not any direct interpretation can be
extracted from Eq. 17, it is emphasized that only
experimental data can provide a robust
interpretation and matching if any, from the
implementation of Bessel functions in the Keller-
Segel scenario. Fig. 2 also exhibits a possible
competitivity among bacteria along their
displacements when all of them are under action of
chemotaxis. This displacement per unit of time
constitutes the aggregation bacteria velocity “ ” as Fig. 3 – The normalized total charge of bacteria against the
written in right-side of Eq. 17. A tentative sphere radius exhibiting oscillations due to the Bessel-like
explanation about the origin of motility in certain behavior.
types of bacteria, would be inside the territory of Thus in those scenarios of high electric charge for
electricity where physics laws could explain example, one can consider the role of
inherent properties that are driven by electric electrodynamics in relation to the level of
forces, either attraction or repulsion. Some studies disruption among populations from the fact that
in the past about that have been reported, for large accumulation of ions would generate electric
example the one given in [11]. Under this view, the forces among them. It should be noted that electric
component ionic of bacteria emerges as the main interactions can be a reason to disturb the purpose
point to board the problem of motility and of colonization. This might affect the “so-called
chemotaxis. With this property, classic cheaters” and other types of social manifestations of
electrodynamics emrges as a sustained scenario to bacteria when carrying out actions of chemotaxis.
go through the bacteria motility properties. Furthermore, engineered nanodevices recovered of
Therefore, one can anticipate that the ionic material would constitute an interesting
displacements done by aggregations of bacteria is window to attack the problem of infection and the
dictated by classic physics and its corresponding respective diseases caused by bacteria (or virus).
electrodynamics. It is actually not valid for With this background, it is feasible to derive a
distances less than 0.001nm where quantum theory of classical electrodynamics from a BKS
mechanics governs. equation as expressed in Eq. 12. Thus, it can be
written below in conjunction with time evolution as:
3. ELECTRODYNAMICS ANALYSIS OF
BESSEL-KELLER-SEGEL EQUATION ( , ) ( , ) ( , )

= [ ] + [ ] + ( − ) ( , ).
A first view to be debated is about the BKS equation’s
solutions as done in Eq. 13 where the integer-order ( )
Bessel functions appear as the possible solutions of As seen in previous works, bacteria can transport
bacteria density. One can wonder if the volume electrically charged proteins and any type of ions
integration returns the total electric charge. Actually, that microorganisms can bring on them. This
this fits well in electrodynamics in the sense that the constitutes an argument to analyze the Keller-Segel
total charge enclosed in a spherical volumen of equation in terms of electric charge.
radius “R” (for example, another spatial geometry
can be opted as well). A straightforward integration:

124 © International Telecommunication Union, 2021